Contacts
Phone: +39.02.2399.8357
Skype: jacopo.pier
E-mail: jacopo.marconi@polimi.it
MeccPhD International Track
Supervisor: Prof. Francesco Braghin
Tutor: Prof. Bianca Maria Colosimo
University of Origin: Politecnico di Milano - Mechanical Engineering
Thesis Title: Parametric Reduced Order Models for Imperfect Structures with Geometric Nonlinearities
Introduction
The Finite Element (FE) method has long been a fundamental analysis and design tool in many areas of science and engineering. In structural mechanics it is almost mandatory to use FE models to investigate the behavior of complex systems, which often have many geometric details that would be difficult to handle with lumped-parameter or analytical models.
However, large FE simulations would often require considerable computational resources and time. This is especially true for nonlinear simulations where, in contrast to linear analysis, the nonlinear force vector and its Jacobian need to be reassembled and evaluated multiple times within Newton-like iteration loops, required to solve the nonlinear system. In some cases, designers may ultimately prefer to perform real experiments rather than numerical ones, if the costs allow.
In this context, often it is mandatory to resort to Reduced Order Models – ROM, which aim to reproduce the behavior of the complete, or Full Order Model – FOM, starting from some inherent property of the latter. The topic has gained increasing momentum in the research community over the last few decades, and many solutions are now available.
In this work, we resort to model-driven methods, which can be envisioned as the extension of modal analysis to the study of the oscillatory behavior of structures undergoing large deflections and strains.
The latter defines what goes under the name of “geometric nonlinearity”.
Objectives
The objective of our research is mainly driven by the needs of the MEMS industry.
In this field we find indeed small thin-walled structures, operating at extremely low pressure, undergoing relatively large displacements: the perfect settings for the onset of nonlinear oscillations. On top of that, the dynamic response of these microstructures is strongly affected by manufacturing imperfections, which are inherent to the production process and cannot be eliminated. The need to deliver products with uniform and predictable performances thus imposes the analysis of defected structures. To address these problems, nonlinearities and defects, we propose to develop a ROM
- which can describe geometric nonlinearities
- which is cheapto construct and to run
- which needs not previous data, coming either from full-order solutions and/or experimental
- which can be used for multiple scenarios
- which can consider the shape variability given by the presence of defects
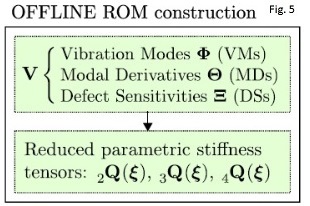
The points above lead us to the development of a class of model-driven Nonlinear Parametric ROM, which we named DpROM.
Methods
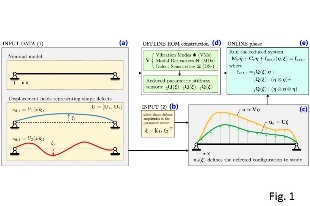
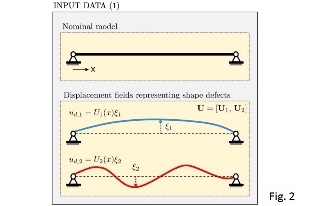
Following Budiansky’s deformation model, the strains of the defected structure can be approximated as:
ε = L1(u) + ½ L2(u) + L11(u,d),
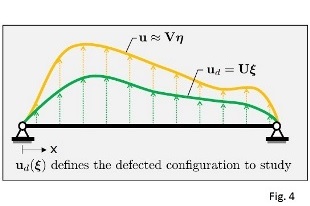
being u and d the real and the defect-induced displacement fields. Later, this result has been generalized to a more rigorous formulation involving a Neuman expansion of the strains, of which Budiansky’s model resulted to be only the zero-th order term. The defect field d can be chosen as a combination of user-defined defects, and the amplitude of each defect is a parameter of the model, which can be changed even after the model is built. After some manipulation and FE discretization, it is possible to write 2nd, 3rd and 4th order reduced stiffness tensors such that:
f˜ = K˜2q + K˜3qq + K˜4qqq
being f˜ the nonlinear elastic internal forces and q the reduced coordinates. In this way, f˜ evaluation is extremely fast, since no reassembling is performed during the solution procedure.
Results
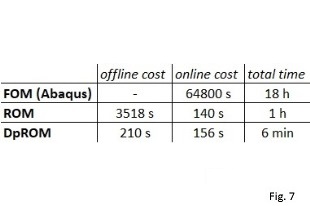
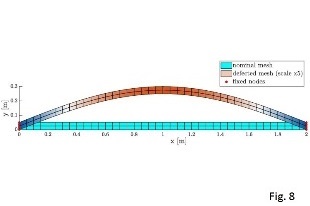
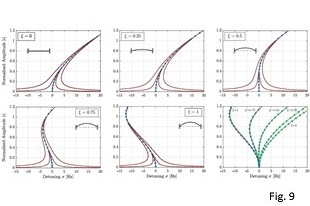
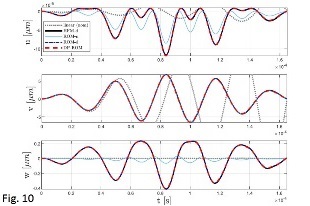
Results are shown in Figg.8-9 (Frequency responses for a straight beam with a arc-like defect. The transition from hardening to softening behavior is well captured by all the tested models) and Fig.10 (Transient simulations and computational times of a MEMS model with 100k dofs), where time and frequency domain analyses have been performed. In both scenarios, the DpROM shows high accuracy and considerably high speed-ups.
Conclusions
In this work a new class of pROMs to address defected structures in nonlinear dynamics have been presented. Using these models, accurate simulations can be carried out in the matter of minutes, whereas the study of the full system is not even possible due to computing limitations, as in the case of frequency responses. The time savings due to the parametric nature of the model, in the author’s vision, will enable the statistical analysis for imperfect structures.
References
J. Marconi, P. Tiso, F. Braghin, A nonlinear reduced order model with parametrized shape defects, CMAME, 2020.
J. Marconi et al., A higher-order parametric nonlinear reduced-order model for imperfect structures using Neumann expansion, Nonlinear Dynamics, 2021
J. Marconi et al., Exploiting Nonlinearities for Frequency-Matched MEMS Gyroscopes Tuning, INERTIAL 2021